Closed Sealed Subwoofer Box Equations Formulas Design Calculator Constant

Low Frequency Enclosures - Car Audio - Home Theater Sound System

Subwoofer Box Comparison Calculator:
Compare bandpass, sealed and vented frequency output graphs
for a subwoofer in one program.

Problem:

Solve for constant.

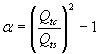
Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Solution In Other Units:

Enter input values and press Calculate.

Input Unit Conversions:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

constant

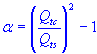	constant
	speaker system total Q at f_c
	speaker total Q at f_s

efficiency bandwidth product

	efficiency bandwidth product
	speaker resonance frequency
	speaker electrical Q

system resonance frequency

	system resonance frequency
	speaker system total Q at f_c
	speaker resonance frequency
	speaker total Q at f_s

minus three decibel half power frequency

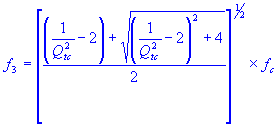	minus three decibel half power frequency
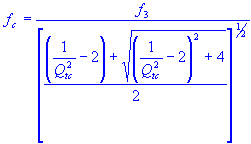	system resonance frequency

net internal box volume

	net box internal volume
	air volume with same acoustic compliance as the speaker suspension
	constant

free air reference efficiency

	free air reference efficiency
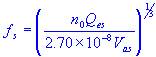	speaker resonance frequency
	air volume with same acoustic compliance as the speaker suspension
	speaker electrical Q

sound pressure level

	sound pressure level
	free air reference efficiency

maximum air volume displaced by cone excursion

	maximum air volume displaced by cone excursion
	cone effective radiation area
	cone peak linear displacement

cone effective radiation area

	cone effective radiation area
	cone diameter plus one third of surround

K ₁ constant

	K₁ constant
	air density
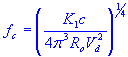	system resonance frequency
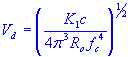	maximum air volume displaced by cone excursion
	sound speed in air

K₂ constant

	K₂ constant
	K₁ constant

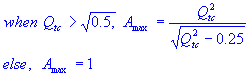A_max constant

maximum displacement limited linear power output

	maximum displacement limited linear power output
	K₁ constant
	A_max constant

required electrical input to achieve P_ar

	required electrical input to achieve P_ar
	maximum displacement limited linear power output
	free air reference efficiency

peak sound pressure level

	peak sound pressure level
	maximum speaker power input

References - Books:

Dickason, Vance. 1991. The Loudspeaker Design Cookbook. Audio Amateur Press. 4th ed.
Steele, Brian. 2002. The Subwoofer DIY Page v1.1. https://www.diysubwoofers.org.

Background

Creating the perfect sound system, whether for a car audio setup or a home theater, starts with understanding the core principles behind speaker design. The sealed or closed subwoofer box is a central piece of this audio puzzle. With this guide derived from AJDesign's Subwoofer Box Design Calculator, we dive deep into the constant equation vital for optimizing your subwoofer's performance.

Subwoofers are specifically designed to reproduce low-frequency sounds, and the quality of these sounds is significantly influenced by the design of the subwoofer enclosure. A closed-sealed subwoofer box is a completely sealed environment that affects the speaker's back wave, contributing to its overall sound quality. The design of such boxes involves intricate calculations to ensure the right balance between box volume, speaker size, and the box's internal pressure.

The Equation

The critical equation in designing a sealed subwoofer box revolves around finding the 'constant' directly influencing the speaker's performance. It is defined as:

α = (Q_tc / Q_ts)² - 1

Here, Qtc is the speaker system's total quality factor at the box's resonant frequency (Fc), and Qts is the speaker's total quality factor at the speaker's resonant frequency (Fs).

How to Solve

Determine the Qts value of the speaker, which the manufacturer typically provides.

Choose a target Qtc value for your design. Common Qtc values range from 0.707 (for a flat response) to 1.3 (for more bass).

Apply these values to the equation to solve for the constant, guiding the other design parameters of your sealed subwoofer box.

Example

Suppose you have a subwoofer with a Qts of 0.55, and you desire a Qtc of 0.707 for a flat response across the bass frequencies. Plugging these values into our formula provides:

α = (0.707 / 0.55)² - 1

Resulting in a constant value that dictates the required volume and dimensions of the sealed box for optimal performance.

Fields and Degrees It is Used In

Acoustical Engineering: Tailoring speaker designs to achieve desired sound characteristics.
Automotive Audio System Design: Creating optimal audio systems within a vehicle's acoustics constraints.
Home Theater System Design: Engineering sound systems for maximum audio quality in home entertainment.
Professional Sound Engineering: Designing concert hall and recording studio audio systems.
Audio Technology Research: Developing new speaker materials and design techniques for better sound reproduction.

Real-life Applications

Car Audio Customization: Enhancing car stereo system's bass and overall audio quality.
Home Theater Setup: Achieving cinema-quality sound within home entertainment systems.
Concert Hall Sound Systems: Optimizing audio design for live performances.
Music Production: Tailoring recording studios for optimal sound capture and playback.
Public Address Systems: Designing efficient PA systems for precise sound reproduction in large areas.

Common Mistakes

Ignoring Box Volume: Misestimating the required volume can drastically affect sound quality.
Overlooking Material Thickness: Failing to account for the material thickness can lead to incorrect internal volume calculations.
Not Considering Speaker Displacement: Forgetting to account for the speaker's physical space within the box.
Overcompensating for Bass Response: Attempting to achieve overly aggressive bass can lead to distorted audio.
Neglecting Sealing: Improper sealing of the box can lead to air leaks, significantly impacting performance.

Frequently Asked Questions

Can I use any speaker in a sealed box design?
While most speakers can technically be housed in a sealed box, optimal performance requires careful selection based on the speaker's Qts value.
How does the box volume affect sound quality?
Larger volumes generally yield lower frequency responses but can lead to less precise bass, whereas smaller volumes provide a tighter but possibly weaker bass.
Is it better to have a higher or lower Qtc value?
This depends on your preference for sound quality. A Qtc of 0.707 is optimal for a flat response, but a higher value can enhance bass.
What materials are best for building a sealed subwoofer box?
Dense, rigid materials like MDF (Medium-Density Fiberboard) are most commonly used for their acoustic properties and durability.
Can I adjust the box volume after construction?
Adjusting volume post-construction is only possible by rebuilding the box. It's crucial to get the calculations right the first time.