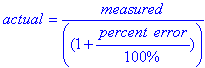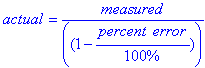Percent Error Equations Formulas Calculator

Math Physics Chemistry Biology Formulas

Solving for percent error.

Inputs:

Can you share this page? Because, it could help others.

Conversions:

measured value

= 0

actual, accepted or true value

= 0

Solution:

percent error = NOT CALCULATED

Change Equation Variable
Select to solve for a different unknown

percent error calculator

Rich internet application version of the percent error calculator.

	Solve for percent error
	Solve for the actual value. This is also called the accepted, experimental or true value. Note due to the absolute value in the actual equation (above) there are two value.
	Solve for the measured or observed value. Note due to the absolute value in the actual equation (above) there are two solutions.

Change Equation to Percent Difference

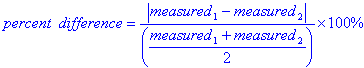Solve for percent difference.

Background:

Percent error is a widely used statistical tool to measure the accuracy of a given value compared to its actual value. This concept is essential in various fields of study and industries as it quantifies the precision of measurements, experiments, or predictions. Understanding and calculating percent error helps professionals and researchers to validate their methodologies, ensure quality control, and enhance the reliability of their findings or products.

Equation:

The percent error is calculated using the equation:

Percent Error = (|Measured Value - Actual Value| / Actual Value) x 100%

Where:

Measured Value is the observed or experimental value.
Actual Value is the known or true value.

How to Solve:

Identify the Measured and Actual Values: Start by pinpointing the experimental (measured) value and the known or textbook (actual) value.

Subtract the Measured Value from the Actual Value: Pay attention to the absolute value here to ensure that the result is non-negative, as percent error is always a positive figure reflecting only the error magnitude, not its direction.

Divide the Difference by the Actual Value: This fraction represents the error relative to the actual value, providing a scale to appreciate the size of the error in context.

Multiply by 100: Converting the result into a percentage rounds off the process, offering a readily interpretable figure that reflects how far off the measurement is in terms of the actual value.

Example:

Suppose a laboratory experiment aims to measure the boiling point of water and records a value of 99°C, whereas the actual boiling point of water under standard atmospheric pressure is 100°C. Applying the formula:

Percent Error = (| 99 - 100 | / 100) x 100% = 1%

This outcome illustrates a 1% error from the actual value, indicating high accuracy in the experimental measurement.

Fields/Degrees It is Used In:

Chemistry: To assess the purity of substances and the precision of chemical measurements.
Physics: In experimental physics, for calculating discrepancies in physical measurements from theoretical expectations.
Engineering: For determining the accuracy of model predictions versus real-world outcomes.
Economics: To evaluate the precision of economic forecasts.
Medicine: This measures errors in diagnostic tests and equipment calibrations.

Real-Life Applications:

Quality Control: Manufacturing industries use percent error to ensure products meet specified tolerances.
Meteorology: In assessing the accuracy of weather forecasts against actual weather conditions.
Navigation: To quantify the accuracy of GPS and other navigational tools.
Finance: For evaluating the accuracy of financial forecasts and models.
Education: Teachers use it to highlight the importance of measurement precision and accuracy in scientific experiments.

Common Mistakes:

Ignoring the Absolute Value: Only using absolute values can correctly yield negative percent errors.
Misidentifying Values: Confusing the measured and actual values can completely skew the results.
Calculation Errors: Simple mathematical mistakes in division or multiplication can lead to incorrect percent errors.
Unit Inconsistencies: Failing to standardize units before calculation can cause errors.
Rounding Too Early: Early rounding in calculations can reduce the accuracy of the final percent error.

Frequently Asked Questions:

Can percent error be negative?
No, percent error is expressed as a positive value since it reflects the magnitude of the error without direction.
What does a 0% percent error indicate?
A 0% percent error signifies perfect accuracy, meaning the measured value matches the actual value exactly.
How significant is a percent error in indicating a measurement problem?
This can vary by field, but typically, a percent error above 10% may warrant a review of the experimental or measurement protocols.
Does a lower percent error always mean better accuracy?
A lower percent error indicates a measurement closer to the actual value, signifying higher accuracy.
Is percent error the same as absolute error?
No, percent error normalizes the absolute error to the magnitude of the actual value, providing a relative measure of error.

Percent Error Equations Calculator