Curb Type Gutter Equations Formulas Design Calculator Flow Rate

Problem:

Solve for gutter flow rate.

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Solution In Other Units:

Enter input values and press Calculate.

Input Unit Conversions:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

curb type gutter

	gutter flow rate
	Manning's coefficient
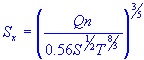	roadway cross slope
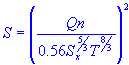	longitudinal slope
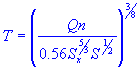	flow width

curb opening inlet with weir operation

	capture flow rate or interception capacity
	curb opening length
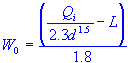	curb opening width
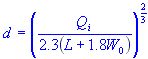	flow depth at curb

curb opening inlet with weir operation
no depression

	capture flow rate or interception capacity
	curb opening length
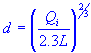	depth of flow

curb opening inlet with orifice operation

	capture flow rate or interception capacity
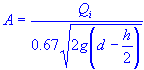	curb opening area
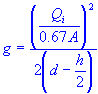	acceleration of gravity
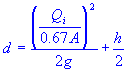	flow depth at curb
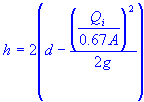	opening height

gutter opening inlet

	capture flow rate or interception capacity
	grate perimeter
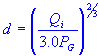	flow depth

slotted pipe drain inlet

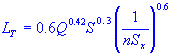	pipe length for complete interception
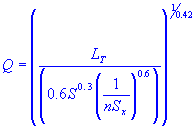	flow rate
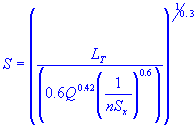	longitudinal slope
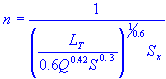	Manning's coefficient
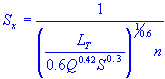	roadway cross slope

gutter capture efficiency

	gutter capture efficiency
	capture flow rate
	total flow rate

gutter carryover or bypass

	gutter carry over or bypass
	total flow rate
	capture flow rate

Where

Q	=	gutter flow rate
n	=	Manning's coefficient
S_x	=	roadway cross slope
S	=	longitudinal slope
T	=	flow width
d	=	flow depth at curb
a	=	depressing depth

References - Books:

Martin Wanielista, Robert Kersten and Ron Eaglin. 1997. Hydrology Water Quantity and Quality Control. John Wiley & Sons. 2nd ed.

Background

The curb gutter equation is critical in civil engineering and stormwater management. It helps engineers calculate the water flow rate in curb and gutter systems, commonly found along streets and highways. These systems are designed to channel rainwater efficiently to prevent flooding and erosion, protect infrastructure, and maintain road safety. Understanding the flow rate in curb gutter systems is essential for designing effective drainage solutions.

Stormwater runoff represents a critical issue in urban environments, especially in areas that experience substantial rainfall or intense storm events. It is essential to address this challenge to mitigate potential adverse effects on infrastructure, ecosystems, and public health. Properly managing this runoff is vital to avoid road flooding and reduce the impact of water on structures and landscapes. The curb gutter equation plays a crucial role in this process by providing a reliable method to estimate the amount of water that flows through a gutter based on various factors, including the gutter's shape, slope, and surface roughness.

Fields/Degrees It Is Used In

Civil Engineering: The curb gutter equation is essential for designing street drainage systems that handle stormwater runoff in urban settings.
Environmental Engineering: It calculates water flow in drainage channels and ensures water management strategies effectively mitigate flooding.
Hydrology: Hydrologists use this equation to model the movement of surface water and its flow through different drainage systems.
Urban Planning: Urban planners use these calculations to design roads, streets, and stormwater infrastructure resilient to heavy rain.
Construction Engineering: In construction, the curb gutter equation helps design gutter systems that prevent water damage to newly built roads and properties.

Real-Life Applications

Urban Stormwater Management: Used to design effective stormwater drainage systems in cities to prevent flooding during heavy rains.
Highway Drainage: Ensures that highways have sufficient drainage along curbs to avoid water accumulation and road damage.
Flood Control Systems: The equation helps design flood prevention systems by controlling water flow in gutters and drainage systems.
Park and Recreation Areas: Ensures drainage systems around parks and recreational areas function correctly to avoid waterlogging and infrastructure damage.
Agricultural Drainage: Applied farmlands to manage water flow in drainage ditches, helping to control waterlogging and erosion.

Common Mistakes

Incorrect Unit Conversion: Using consistent units for perimeter, hydraulic radius, or slope can lead to correct calculations.
Ignoring Surface Roughness: The equation assumes standard conditions, but rough surfaces (such as debris) can affect flow rates, requiring adjustments.
Underestimating the Impact of Slope: The gutter's slope significantly affects the flow rate; underestimating its value can lead to design failures.
Failure to Account for Curb Shape: The shape of the curb can influence the flow, and ignoring this can lead to inaccurate calculations.
Misinterpreting the Hydraulic Radius: The hydraulic radius often needs to be clarified with the flow depth; improper estimation can lead to significant errors.

Frequently Asked Questions (FAQs)

What is the hydraulic radius, and why is it important?
The flow's cross-sectional area ratio to the wetted perimeter is the hydraulic radius. It is crucial because it directly affects the velocity and flow rate in the gutter system.
How do I measure the perimeter of the gutter?
The perimeter is the total length of wetted surfaces, like the bottom and sides, in contact with water during flow.
Can I use this equation for all types of gutters?
This equation is generally used for standard curb gutters, but adjustments may be needed for irregular shapes or conditions, such as steep slopes or debris-filled gutters.
What happens if the slope is too steep?
If the slope is too steep, the flow rate may exceed the gutter's capacity, leading to overflow. It's essential to balance slope and gutter size for optimal flow.
How does surface roughness affect the equation?
Surface roughness can increase friction, reducing the actual flow rate compared to the theoretical value. Adjusting for rough surfaces in real-world applications is essential.