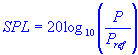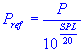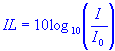Sound Wave Equations Calculator
Science Physics Formulas
Problem:
Solve for Sound Pressure Level SPL
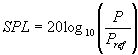
Enter Calculator Inputs:
Can you share this page? Because, it could help others.
Solution:
Solution In Other Units:
Input Unit Conversions:
Change Equation or Formulas:
Tap or click to solve for a different unknown or equation
 | sound pressure level |
 | sound pressure |
 | reference pressure |
 | sound intensity level |
 | sound intensity |
 | reference intensity |
 | intensity at a distance from point source |
 | distance from sound source |
 | power emitted |
 | wave frequency |
 | wave velocity |
 | wavelength |
 | noise pollution level NPL |
| SPL | = | sound pressure level, decibels (db) |
| P | = | sound wave pressure, newtons/meter2 |
| Pref | = | reference pressure or hearing threshold, newton/meter2 |
| IL | = | intensity level, decibel (db) |
| I | = | sound intensity, watt |
| I0 | = | reference intensity or least audible sound level, watts |
| PAV | = | average power, watt |
| NPL | = | noise pollution level, decibel (db) |
Notes:
- Usually, I0 is set to 10-12 watts
- Usually, Pref is set to 0.00002 newtons/meter2
References - Books:
- P. Aarne Vesilind, J. Jeffrey Peirce and Ruth F. Weiner. 1994. Environmental Engineering. Butterworth Heinemann. 3rd ed.
- Tipler, Paul A.. 1995. Physics For Scientists and Engineers. Worth Publishers. 3rd ed.
Background
Sound Pressure Level (SPL) is an essential concept in acoustics, measuring the sound pressure relative to a reference pressure. It is expressed in decibels (dB), giving a logarithmic measure of the ratio of two pressures. The reference pressure, Pref, is typically taken as 20 micropascals in air, considered the threshold of human hearing.
Equation
The formula to calculate the sound pressure level (SPL) is:
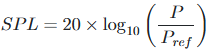
where:
- SPL is the sound pressure level in decibels (dB)
- P is the actual sound pressure in pascals
- Pref is the reference sound pressure (20 micropascals)
How to Solve
To solve for SPL:
Measure the actual sound pressure (P) at the point of interest.
Use the reference pressure Pref = 20 x 10-6 pascals.
Plug these values into the SPL formula:
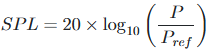
Example
Suppose the measured sound pressure (P) is 0.2 pascals. Calculating SPL:
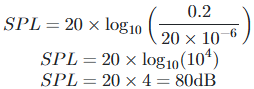
Fields/Degrees Where It Is Used
- Acoustical Engineering: Designing audio equipment, soundproofing, and room acoustics.
- Environmental Science: Monitoring and controlling noise pollution.
- Automotive Engineering: Designing quieter vehicles and evaluating engine sounds.
- Audiology: Assessing hearing health and managing hearing aids.
- Architecture: Incorporating sound considerations in buildings and public spaces.
Real-Life Applications
- Hearing Aids: Tuning hearing aids to compensate for particular hearing loss levels.
- Concert Halls: Designing spaces to optimize acoustics for various performances.
- Sound Level Meters: These are used in environmental assessments to ensure compliance with noise regulations.
- Home Appliances: Assessing noise levels to meet consumer preferences for quieter products.
- Workplace Safety: Ensuring that industrial workplaces comply with sound exposure standards to prevent hearing loss.
Common Mistakes
- Not accounting for environmental factors like temperature or humidity can affect sound measurements.
- Using incorrect reference pressure not corresponding to the media being measured.
- Confusing sound pressure with sound power or intensity is a different aspect of sound.
- Neglecting the calibration of sound-measuring devices leads to inaccurate readings.
- Rounding off values too early in the calculations can lead to significant errors.
Frequently Asked Questions with Answers
- What is the reference sound pressure used for SPL, and why?
The reference sound pressure is 20 x 10-6 pascals, chosen as it represents the threshold of human hearing, below which sound is inaudible to most people. - Can SPL be negative?
Yes, SPL can be negative if the sound pressure is lower than the reference pressure; however, this is typically inaudible to humans. - How does temperature affect SPL measurements?
SPL is less affected, but the speed of sound varies with temperature, potentially affecting measurements involving distance or sound propagation. - Why use a logarithmic scale for sound pressure?
Human perception of loudness is more aligned with a logarithmic scale, making the dB scale a more practical measure of perceived loudness than a linear scale. - Is SPL the same underwater?
The concept is the same, but the reference pressure and the medium's acoustic properties differ, necessitating special considerations in underwater acoustics.
Online Web Apps, Rich Internet Application, Technical Tools, Specifications, How to Guides, Training, Applications, Examples, Tutorials, Reviews, Answers, Test Review Resources, Analysis, Homework Solutions, Worksheets, Help, Data and Information for Engineers, Technicians, Teachers, Tutors, Researchers, K-12 Education, College and High School Students, Science Fair Projects and Scientists
By Jimmy Raymond
Contact: aj@ajdesigner.com
Privacy Policy, Disclaimer and Terms
Copyright 2002-2015