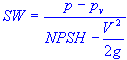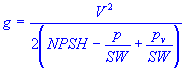Pump Equations Formulas Calculator
Fluid Mechanics and Hydraulics
Problem:
Solve for Water Horsepower
Enter Calculator Inputs:
Can you share this page? Because, it could help others.
Solution:
Solution In Other Units:
Input Unit Conversions:
Change Equation or Formulas:
Tap or click to solve for a different unknown or equation
 | Solve for water horsepower |
 | Solve for flow rate or discharge |
 | Solve for total head |
 | Solve for pump efficiency |
 | Solve for brake horsepower |
 | Solve for NPSH - net positive suction head |
 | Solve for fluid or liquid velocity |
 | Solve for pressure at impeller inlet |
 | Solve for fluid or liquid vapor pressure |
 | Solve for specific weight of fluid or liquid |
 | Solve for the acceleration of gravity |
| WHP | = | water horsepower |
| Q | = | flow rate or discharge |
| H | = | total head |
| n | = | pump efficiency |
| BHP | = | brake horsepower |
| NPSH | = | net positive suction head |
| V | = | velocity of fluid or liquid |
| p | = | impeller inlet pressure |
| pv | = | vapor pressure of fluid or liquid |
| SW | = | specific weight of fluid or liquid |
| g | = | acceleration of gravity |
References - Books
P. Aarne Vesilind, J. Jeffrey Peirce and Ruth F. Weiner. 1994. Environmental Engineering. Butterworth Heinemann. 3rd ed.
Background
Water horsepower (WHP) is a term used to describe the power transferred to water by a pump, turbine, or other hydraulic machines. The concept is crucial in hydrodynamics and hydraulic systems design, directly linking the mechanical energy transferred to or from water to the physical properties of fluid flow. Understanding WHP is essential for efficient and effective hydraulic machinery design, operation, and optimization.
Equation
The standard equation used to solve for water horsepower (WHP) is:
WHP = Q x H / 3960
where:
- WHP is the water horsepower
- Q is the discharge or flow rate in gallons per minute (GPM)
- H is the total head in feet
- 3960 is a constant that results from the conversion factors between gallons, minutes, feet, and the definition of horsepower
How to Solve
To solve for WHP, you need to follow these steps:
- Measure or Determine Flow Rate (Q): The volume of water moving through the system is measured in gallons per minute (GPM).
- Ascertain Total Head (H): The total head in a hydraulic system represents the height in feet that the pump needs to lift the water. It includes both elevation difference and friction losses.
- Plug Values into the Equation: Insert your Q and H values into the WHP equation.
- Calculate: Divide the product of Q and H by 3960 to find the water horsepower.
Example
Suppose a pump moves 500 gallons of water per minute (GPM) against a total head of 100 feet. Find the WHP.
Plugging the values into the equation:
WHP = 500 x 100 / 3960
WHP = 50000 / 3960
WHP = 12.63
The water horsepower in this scenario is approximately 12.63.
Fields/Degrees It Is Used In
- Mechanical Engineering: Mechanical engineers often need to calculate water horsepower for pump and turbine design and testing.
- Civil Engineering: It's used in designing municipal water supply and wastewater treatment systems.
- Environmental Engineering: Understanding WHP is critical in designing systems for environmental protection, such as hydroelectric power plants.
- Agricultural Engineering: In irrigation systems, calculating WHP is necessary for pump selection and system design.
- Marine Engineering: For the design and analysis of shipboard hydraulic systems, such as ballast and bilge systems.
Real-Life Applications
- Pumping Systems: Calculating the WHP required to pump water from a source to its destination in applications ranging from agriculture to municipal water supply.
- Hydroelectric Power Plants: Determining the power generated from falling water.
- Water Treatment Plants: For moving water through filtration and purification processes.
- Irrigation Systems: In agriculture, for the design of pumps to distribute water efficiently.
- Fountain Design: Calculating the power required to achieve desired water effects in decorative fountains.
Common Mistakes
- Incorrect Units: Using the wrong units for flow rate or head can drastically change the calculation. Always use gallons per minute and feet, respectively.
- Overlooking Friction Losses: Failing to account for friction losses in total head can lead to underestimating WHP.
- Misinterpreting Total Head: Confusing elevation head with total head, which includes pressure, velocity, and elevation components.
- Neglecting Efficiency: WHP is the ideal power. The actual power needs to consider the efficiency of the hydraulic machinery.
- Rounding Errors: Small rounding errors in large-scale applications can lead to significant inaccuracies.
Frequently Asked Questions
- What's the difference between WHP and Brake Horsepower (BHP)?
WHP measures the power transferred to the water, whereas BHP is the total power output of the engine or motor, taking into account efficiency losses. - Can WHP be converted to electrical or mechanical horsepower?
Yes, WHP can be converted to electrical or mechanical horsepower, but those conversions must consider system efficiency. - What happens if my application is in metric units?
If working in metric units, you need to convert to the appropriate units (cubic meters per second for flow rate and meters for head) and adjust the constant in the formula accordingly. - Is it possible for WHP to be zero?
Yes, if there is no flow (Q=0) or no head (H=0), WHP would be zero, indicating no work is done on the water. - How does the efficiency of a pump affect WHP calculations?
WHP provides a theoretical value. A pump's efficiency determines how much actual power (BHP) needs to be provided to achieve the calculated WHP. Lower efficiency requires more BHP for the same WHP.
Online Web Apps, Rich Internet Application, Technical Tools, Specifications, How to Guides, Training, Applications, Examples, Tutorials, Reviews, Answers, Test Review Resources, Analysis, Homework Solutions, Worksheets, Help, Data and Information for Engineers, Technicians, Teachers, Tutors, Researchers, K-12 Education, College and High School Students, Science Fair Projects and Scientists
By Jimmy Raymond
Contact: aj@ajdesigner.com
Privacy Policy, Disclaimer and Terms
Copyright 2002-2015