Manning Equations Formulas Calculator

Fluid Mechanics Hydraulics

Problem:

Solve for Flow Velocity.

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Solution In Other Units:

Enter input values and press Calculate.

Input Unit Conversions:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

	Solve for flow velocity
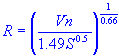	Solve for hydraulic radius
	Solve for energy grade line slope
	Solve for roughness coefficient

Where

V	=	flow velocity
R	=	hydraulic radius
s	=	energy grade line slope
n	=	coefficient of roughness

References - Books:

Warren Viessman, Jr, Mark J. Hammer. 1993. Water Supply and Pollution Control. Harper Collins College Publishers. 5th ed.

Background

The Manning equation is widely used in hydrology and open channel flow to calculate water flow velocity. It's an empirical equation that accounts for the roughness of the channel's surface, the hydraulic radius, and the energy grade line slope. Understanding this formula is crucial for designing efficient water conveyance systems like sewers, irrigation channels, and culverts.

Understanding and applying the Manning equation correctly can significantly impact the design and analysis of hydraulic systems. Careful consideration of the equation's variables and their accurate measurement is crucial for its successful application.

Equation

The Manning equation is expressed as:

V = R^2/3S^1/2/n for hydraulic radius in meters
V = 1.486R^2/3S^1/2/n for hydraulic radius in feet

Where:

V is the flow velocity (m/s or ft/s)
n is Manning's roughness coefficient
R is the hydraulic radius (m or ft), typically the flow cross-sectional area divided by the wetted perimeter
S the energy grade line slope (dimensionless) is essentially the channel's slope

How to Solve

Determine the Hydraulic Radius (R): Calculate the cross-sectional area of water flow and divide it by the wetted perimeter. For a rectangular channel, for example, R would be the area of water (width times depth) divided by the wetted perimeter (width + 2 times depth).

Identify the Slope (S): Measure the elevation drop over a certain distance along the channel. Divide the elevation drop by the distance to get the slope.

Obtain Manning's Roughness Coefficient (n): This value depends on the channel's material and can be obtained from standard tables.

Solve the Equation: Substitute the values of R, S, and n into the Manning equation to calculate the flow velocity (V).

Example

Suppose we have a concrete channel where:

The hydraulic radius (R) is 0.5 m,

The slope (S) is 0.01,

Manning's roughness coefficient (n) is 0.013 for concrete.

Plugging these values into the Manning equation:

[V = \frac{1}{0.013} \times (0.5)^{2/3} \times (0.01)^{1/2}]

[V ≈ 1.17, m/s]

So, the flow velocity would be approximately 1.17 m/s.

Fields/Degrees It's Used In

Civil Engineering: Designing and analyzing water conveyance systems like culverts and storm sewers.
Environmental Engineering: Studying natural water bodies and creating sustainable solutions for flood control.
Agricultural Engineering: Developing efficient irrigation canals and drainage systems for farms.
Hydrology: Understanding the movement and distribution of water in natural and artificial channels.
Urban Planning: Designing urban stormwater management systems to prevent flooding and erosion.

Real-Life Applications

Irrigation Canals: Calculating the optimal flow velocity to design canals that efficiently distribute water.
Sewer Systems: Designing sewer lines with appropriate flow velocities to avoid sediment deposition and blockages.
Flood Control Channels: Planning channels that can safely carry floodwaters away from populated areas.
Culverts: Designing culverts under roads to pass drainage water without causing erosion or road damage.
Stream Restoration: Restoring streams and their banks to prevent erosion and promote healthy ecosystems by understanding flow dynamics.

Common Mistakes

Incorrect (R) Calculation: Not correctly calculating the wetted perimeter or cross-sectional area of flow.
Wrong (n) Value: Using an inappropriate roughness coefficient for the channel material or condition.
Assuming Uniform Flow: Applying the equation without considering flow or channel slope variations.
Overlooking Units: Mixing units (metric and imperial) can lead to significant errors in the calculation.
Neglecting Slope Variations: Using an average slope for the entire channel instead of accounting for variations that can affect the flow velocity.

Frequently Asked Questions

Can the Manning equation be used for any fluid?
It's primarily used for water. It assumes specific properties of water, making it less accurate for other fluids.
How do I determine my channel's best value of (n)?
Use published tables and guides based on empirical data. Consider the material and the level of vegetation or debris.
Is the Manning equation accurate for steep slopes?
It can be less accurate for very steep slopes, as it assumes uniform and steady flow, which may not be the case.
Can I use the Manning equation for pipe flow?
Yes, but the hydraulic radius is calculated differently (it's typically one-fourth of the pipe diameter for full flow conditions), and considerations for pipe flow should be taken.
What if my channel isn't uniform?
Divide the channel into segments where conditions are relatively uniform and apply the Manning equation to each segment.