Hazen Williams Equations Formulas Calculator

Hydraulics and Fluid Mechanics Formulas

Problem:

Solve for flow mean velocity

Note: Valid only for ambient temperatures and turbulent flow

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Solution In Other Units:

Enter input values and press Calculate.

Input Unit Conversions:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

Mean Fluid Velocity

	mean flow velocity
	friction coefficient
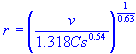	hydraulic radius
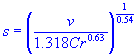	hydraulic grade line slope

Fluid Flow Rate

	discharge or flow rate
	friction coefficient
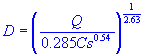	pipe diameter
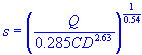	hydraulic grade line slope

Where

v	=	mean flow velocity
C	=	Hazen Williams friction coefficient
r	=	hydraulic radius
s	=	hydraulic grade line slope
Q	=	flow rate or discharge
D	=	pipe diameter

Reference - Books:

P. Aarne Vesilind, J. Jeffrey Peirce and Ruth F. Weiner. 1994. Environmental Engineering. Butterworth Heinemann. 3rd ed.

Background

The Hazen-Williams equation is a well-known empirical formula commonly used in hydraulic engineering, particularly for calculating pressurized water flow within pipes. Unlike more complex models like the Darcy-Weisbach formula, the Hazen-Williams is favored for its simplicity and accuracy in scenarios with ambient temperatures and turbulent flow conditions.

The Hazen-Williams equation provides a practical and straightforward method for calculating water flow velocity in hydraulic engineering. Professionals can design efficient and effective water movement systems for various practical applications by understanding and accurately applying the formula.

Equation

The formula to compute the mean flow velocity of water in a pipe using the Hazen-Williams equation is given by:

v = 0.849 x C^1.852 x r^0.634 x s^0.54

Where:

v is the mean flow velocity (in meters per second)
C is the Hazen-Williams friction coefficient (dimensionless)
r is the hydraulic radius of the pipe (in meters)
s is the hydraulic grade line slope (dimensionless)

How to Solve

To solve the equation for mean flow velocity:

Identify Parameters: Based on the system specifications and conditions, determine the values of C, r, and s.
Input Values: Substitute these values directly into the equation.
Calculation: Compute according to the formula using a calculator or appropriate software to find v.

Example

Consider a pipe with a hydraulic radius (r) of 0.15 meters, a Hazen-Williams coefficient (C) of 100, and a slope (s) of 0.02. Substituting these values into the equation gives:

v = 0.849 x 100^1.852 x 0.15^0.634 x 0.02^0.54

v ≈ 1.19 meters per second

This means the mean flow velocity is approximately 1.19 meters per second.

Fields/Degrees It Is Used In

Civil Engineering: Design and analysis of municipal water supply systems.
Environmental Engineering: Assessment of wastewater treatment and stormwater management.
Agricultural Engineering: Irrigation systems planning and optimization.
Mechanical Engineering: Cooling systems design involving water transportation.
Construction Management: Oversight of infrastructure projects requiring fluid mechanics knowledge.

Real-Life Applications

Urban Water Distribution Networks: Ensuring efficient water delivery to residential and commercial areas.
Fire Suppression Systems: Designing pipe networks for optimal water pressure and flow.
Irrigation Channels: Maximizing coverage and minimizing water waste in agricultural settings.
Flood Risk Management: Designing levees and drainage systems to handle storm surges.
Industrial Cooling Systems: Maintaining systems for heat exchange and process cooling in factories.

Common Mistakes

Incorrect Coefficient: Using an inappropriate C value unsuitable for the pipe material or condition.
Misjudged Hydraulic Radius: Miscalculating r, ignoring that it involves the interior pipe surface and the water level.
Neglecting Temperature Effects: Forgetting that the equation is primarily valid for ambient temperature waters.
Decimal Misplacement: Simple decimal errors can lead to significant discrepancies in the outcome.
Overlooking Turbulence: Assuming the equation works for laminar flow, it is designed for turbulent conditions.

Frequently Asked Questions with Answers

Can the Hazen-Williams equation be used for gases?
No, this equation is calibrated explicitly for liquids, particularly water.
What is the meaning of the hydraulic grade line slope?
It represents the slope of the energy line of the water flowing in the pipe, proportional to the energy loss per unit length.
Is the Hazen-Williams suitable for all temperatures?
It is ideally used only for water around ambient temperature ranges.
Can this be applied to any pipe material?
Yes, but the C value must accurately reflect the material and condition of the pipe.
What does a higher C value indicate?
A higher C value suggests less resistance and smoother pipe material, resulting in greater flow velocity.

Hazen Williams Equations Calculator

Problem:

Enter Calculator Inputs:

Solution:

Solution In Other Units:

Input Unit Conversions:

Change Equation or Formulas:

Reference - Books:

Background

Equation

How to Solve

Example

Fields/Degrees It Is Used In

Real-Life Applications

Common Mistakes

Frequently Asked Questions with Answers