Capital Recovery Compounding Discount Factor Equation Formula Calculator

Economics Formulas - Discrete Compounding Discount Factors

Problem:

Solve for capital recovery factor.

Note: Enter interest(i) in decimal form. For example, an interest rate of 15% would be entered as 0.15

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

Discrete Compounding Discount Factors

		capital recovery
		single payment compound amount
		single payment present worth
		uniform gradient future worth
		uniform gradient present worth
		uniform gradient uniform series
		uniform series compound amount
		uniform series present worth
		uniform series sinking fund

References - Books

Lindeburg, Michael R. 1992. Engineer In Training Reference Manual. Professional Publication, Inc. 8th Edition.

Background

The concept of capital recovery is integral in financial planning and investment analysis. It represents the process of recouping the initial outlay of an investment over a specified period, including the return on investment (ROI). The capital recovery factor (CRF) is a crucial tool used in this process, providing a coefficient that, when multiplied by the initial investment, reveals the annual payment required to recover the investment and its expected returns. This concept is based on the time value of money, which says a dollar today is worth more than a dollar in the future because of its potential earning capacity.

Equation

The capital recovery factor is solved using the equation:

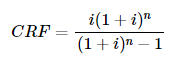
Where:

CRF is the capital recovery factor.
r is the interest rate per period.
n is the number of periods.

How to Solve

To solve for the capital recovery factor:

Determine the Interest Rate and Number of Periods: Establish your periodic interest rate (r)) and the total number of payment periods (n).
Convert Interest Rate to Decimal Form: Ensure the interest rate is expressed as a decimal (e.g., 5% becomes 0.05).
Apply the Formula: Plug the values of r and n into the formula to find the CRF.

Example

Consider you need to recover an investment over 5 years with an annual interest rate of 5%.

Given: r = 0.05 , n = 5

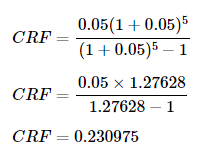
capital recovery factor equation example

Thus, the capital recovery factor is 0.230975.

Fields/Degrees It is Used In

Finance and Accounting: This is used to calculate ROI and loan amortizations.
Real Estate Management: Determining the profitability of property investments.
Engineering Economics: For analyzing the cost-effectiveness of engineering projects.
Environmental Science: Calculating the recovery cost of environmental restoration investments.
Healthcare Management: In budgeting for equipment acquisition and replacement.

Real Life Applications

Loan Amortization Schedules: Computing the periodic payments required to repay a loan.
Pension Fund Management: Determining how much employers need to contribute to ensure pension funds are adequately capitalized.
Equipment Purchase Decisions in Healthcare: Assessing how much annual savings or income is needed to justify new medical equipment.
Property Investment Analysis: Evaluate rental properties to determine if the income generated covers the recovery of the initial investment and its return.
Sustainability Projects: Estimating the annual financial returns from sustainability initiatives to recover the initial outlay.

Common Mistakes

Forgetting to Convert the Interest Rate: Not adjusting the percentage to a decimal when plugging into the formula.
Mixing Up Periods and Rates: Confusing annual rates with monthly or quarterly rates without appropriate adjustments.
Ignoring Compounding Frequency: Failing to align the interest rate and number of periods with the compounding frequency.
Simplistic View on Cash Flows: Overlooking that real-life investments might generate variable, not fixed, annual returns.
Miscalculating Number of Periods: Occasionally, the total investment duration is wrongly counted, affecting the CRF calculation.

Frequently Asked Questions with Answers

What happens to CRF if the interest rate is zero?
The CRF becomes 1/n, implying equal payments over n periods will recover the capital.
Can CRF be used for any interest rate?
Yes, but the rate and periods used in the formula must match in terms of compounding (e.g., both annual).
What does a higher CRF indicate?
A higher CRF suggests a higher annual payment than the principal, usually due to a higher interest rate or shorter duration.
Is CRF applicable to diminishing balance loans?
While it's mainly designed for fixed annuity calculations, modifications can be made for varying payment structures, though CRF is best applied directly to even cash flows.
How does inflation affect the CRF?
Inflation can erode the actual value of future payments. The interest rate should incorporate expected inflation to maintain the investment's real value over time.

Capital Recovery Factor Equations Calculator