Circle Equations Formulas Geometry Calculator

Math Geometry

Problem:

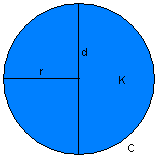
Solve for circle diameter.

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

Circle

	diameter
	radius

	circumference
	radius

	circumference
	diameter

	circumference
	area

	area
	radius

	area
	diameter

	area
	circumference
	radius

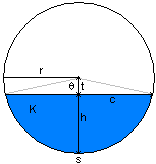
Segment of a Circle

	chord length
	circle radius
	circle center to chord midpoint distance

	segment area
	circle radius

	central angle
	arc length
	circle radius

	segment height
	circle radius
	circle center to chord midpoint distance

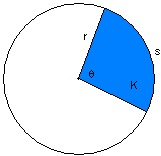
Sector of a Circle

	sector area
	circle radius
	central angle

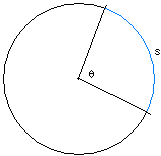
Arc of a Circle

	arc length
	circle radius
	central angle

Background

A circle is a fundamental geometric shape consisting of points equidistant from a fixed central point, known as the radius (r). The diameter (d) spans the circle, stretching through the center with its endpoints on its perimeter. Understanding how radius and diameter are related is essential in geometry and has many scientific and practical uses.

Equation

The formula for finding the diameter of a circle from its radius is simple:

d = 2r

This equation specifies that the diameter (d) is twice the radius (r). This relationship remains the same in all circles, regardless of their size.

How to Solve

Calculating the diameter when the radius is known involves a simple multiplication:

Start with the formula: Begin with the equation d = 2r.
Enter the radius value: Input the radius value where (r) is in the formula.
Multiply: Multiply the given radius by 2.
Find the diameter: The product is the circle's diameter.

Example

A circle has a 4-inch radius. To find the diameter:

d = 2r

Insert the known radius:

d = 2 x 4 inches

Thus, the circle's diameter is:

d = 8 inches

Fields/Degrees It Is Used In

Mechanical Engineering: Designing components with rotational symmetry, such as wheels, pulleys, and bearings, is essential.
Medicine: This technology is helpful in medical imaging because it is crucial to understand the size of circular objects like tumors for planning treatments.
Astronomy: Employed while measuring and understanding celestial objects and their movements within the cosmos.
Urban Planning: Designing curved roadways, rotundas, and roundabouts ensures smooth traffic flow.
Computer Graphics: Integral to algorithm development that involves rendering circular objects and arcs in digital imagery.

Common Mistakes

Mixing Radius and Diameter: Using the wrong diameter or radius can lead to accurate results.
Incorrect Measurements: Failing to measure the radius accurately from the exact center to the perimeter can lead to wrong outcomes.
Formula Confusion: Misapplying the formula meant for circumference or area while trying to find the diameter.
Miscalculations: Simple arithmetic errors during multiplication can yield incorrect diameters.
Neglecting Units: Different or incoherent use of units (e.g., mixing centimeters with inches) can disrupt the equation's balance.

Frequently Asked Questions

Can the diameter be smaller than the radius? No, the diameter is always twice the radius; hence, it is always larger or equal (in hypothetical zero radius cases).
What happens if I measure the diameter but need the radius? Divide the diameter by 2 to get the radius.
Is the formula different if the circle's diameter crosses it multiple times? No, regardless of position, the formula (d = 2r) always applies as it is derived from the geometric properties of a circle.
How can I ensure accurate radius measurement in a practical scenario? It's important to use accurate measuring tools, such as a caliper, to measure the circumference of a circle from different points to the center and calculate the average measurement, if possible.
Does this formula work for ellipses or other round shapes? The formula only applies to perfect circles, not ellipses, with different measurements and requiring different calculations.

Circle Equations Formulas Calculator