Bank Discount Calculator - Real Estate Investment Equations Formulas

Financial Investment Real Estate Property Land Residential Commercial Building Formulas

Problem:

Solve for bank discount.

Enter Calculator Inputs:

Can you share this page? Because, it could help others.

Solution:

Enter input values and press Calculate.

Change Equation or Formulas:

Tap or click to solve for a different unknown or equation

	bank discount
	note maturity value
	annual bank discount rate
	time in years

	bank proceeds
	note maturity value
	bank discount

	bank proceeds
	note maturity value
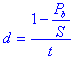	annual bank discount rate
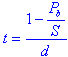	time in years

References - Books:

Burrell, Jamaine. 2007. The Real Estate Math Handbook Simplified Solutions of the Real Estate Investor. Atlantic Publishing Group, Ocala Florida.

Background

Understanding the concept of Bank Discount (D) is crucial in finance and investment. This concept is fundamental in calculating the actual cost or yield of short-term financial instruments like Treasury bills and commercial paper.

The Bank Discount Rate is a simple interest rate used to discount instruments before maturity. The bank discount formula helps determine the bank's discount (D), which is essentially the interest amount deducted in advance on loans or the income earned from investment securities like bonds.

Equation

The formula to calculate the bank discount (D) is as follows:

D = S x d x t

Where:

D = Bank discount
S = Note maturity value (the face value or the amount that will be received at maturity)
d = Annual bank discount rate (expressed as a decimal)
t = Time in years until maturity

How to Solve

To solve for the bank discount (D), follow this simple process:

Identify the note's maturity value (S), the annual bank discount rate (d), and the time in years (t) from the given information.
Convert the annual bank discount rate from a percentage to a decimal by dividing by 100.
Substitute the values of S, d, and t into the equation (D = S x d x t).
Multiply the values to find the bank discount (D).

Example

Suppose a Treasury bill has a face value of $10,000, a bank discount rate of 2%, and matures in 6 months (0.5 years). Calculate the bank discount (D).

Convert the discount rate: d = 2% = 0.02

Substitute the values into the equation: D = 10,000 x 0.02 x 0.5

Calculate: D = 100.

Therefore, the bank discount (D) is $100.

Fields/Degrees It Is Used In

Finance: For calculating yields on short-term investments.
Banking: In loan agreements and for valuing treasury bills.
Investment Banking: For pricing debt instruments.
Economics: Understanding the flow and value of money over time.
Accountancy: In financial reporting and analysis.

Real-life Applications

Investment Evaluation: Helps investors determine the actual yield of short-term treasury bills.
Cost of Short-term Borrowing: Businesses calculate the cost of borrowing via commercial paper.
Treasury Management: Companies assessing their liquidity position.
Loan Pricing: Banks offer rates to borrowers based on discount rates.
Portfolio Management: Investors managing short-term investment portfolios.

Common Mistakes

Incorrect Time Frame: Not converting the investment time into years can lead to wrong calculations.
Decimal Conversion: Forgetting to convert the discount rate from a percentage to a decimal.
Incorrect Values: Mixing up the maturity value (S) and the present value.
Math Errors: Simple calculation errors can lead to significantly incorrect results.
Annualization Mistake: Not adjusting the equation for securities maturing in less than a year.

Frequently Asked Questions

What if the time is in months instead of years?
Convert the time to years by dividing the months by 12 before using it in the formula.
Can the bank discount formula be used for any investment?
It is primarily used for short-term investments like Treasury bills and commercial paper, not for long-term bonds or equities.
Is the bank discount the same as the yield?
No, the bank discount does not account for the compounding of interest, making it different from the yield on an investment.
What does a high bank discount rate indicate?
A higher bank discount rate indicates a lower selling price for the investment, implying higher yields for the investor.
Can the bank discount be negative?
Theoretically, no. It represents the interest deducted upfront or income earned, which wouldn't make sense if it were negative.

Bank Discount Equations Calculator