Passive Crossover Design Equations Formulas Calculator - Two Way First Order Network Butterworth

Car Audio - Speaker - Subwoofer - Electronics

Change Network Order to
Two Way
First | Second | Third | Fourth

Butterworth:
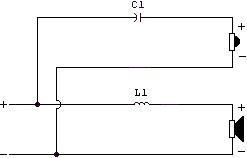
C1 = 0.159 /(R_Hf)
L1 = R_L/(6.28*f)

Two Way First Order Network

Problem:

Calculate the values for a passive two-way first-order network crossover for speakers using the Butterworth filter design.

Inputs:

R_H (High Frequency Impedance)

ohms

R_L (Low Frequency Impedance)

ohms

f (Crossover Frequency)

Can you share this page? Because, it could help others.

Solution:

C₁ Value	----
L₁ Value	----

References - Books:

Tipler, Paul A.. 1995. Physics For Scientists and Engineers. Worth Publishers. 3rd ed.

Background:

The Two-Way First Order Network Equations derived from the Butterworth filter design are fundamental in designing crossover networks for audio systems. These equations play a crucial role in determining the values of capacitors and inductors necessary to achieve the desired crossover frequency and characteristics in a two-way speaker system. By utilizing these equations, engineers and designers can ensure efficient frequency separation and optimize the audio performance of speaker systems.

By applying these calculations and considerations in practical scenarios, designers and engineers can tailor crossover networks to meet specific requirements and optimize the audio performance of speaker systems effectively.

Equations:

The equations essential for calculating the values of capacitor (C1) and inductor (L1) in a two-way speaker system are as follows:

For capacitor C1 = 0.159 / (R_H x f)

For inductor L1 = R_L / (6.28 x f)

How to Solve:

To apply the Two-Way First Order Network Equations to a practical scenario, the following steps can be followed:

Identify the high-pass filter resistance (RH), low-pass filter resistance (RL), and crossover frequency (f).
Substitute the values into the respective equations to calculate the capacitor (C1) and inductor (L1) values required for the crossover network design.
The calculated values can be used to construct the crossover network in the speaker system, thereby achieving the desired frequency separation and audio performance.

Example:

Suppose the high-pass filter resistance R_H = 8 Ω, the low-pass filter resistance R_L = 4 Ω, and the crossover frequency f = 2 kHz. We can calculate the values of capacitor (C1) and inductor (L1) using the given equations:

Calculate the value of capacitor C1:

C1 = 0.159 / (8 x 2,000)
C1 = 0.159 / 16,000
C1 = 0.0000099375 F

Calculate the value of inductor L1:

L1 = 4 / (6.28 x 2,000)
L1 = 4 / 12,560
L1 = 0.000318471 H

Therefore, for the given example, the calculated values are approximately:

C1 = 0.0000099375 F
L1 = 0.000318471 H

These values can be used to design the crossover network for the two-way speaker system, ensuring efficient frequency separation and audio reproduction.

Fields / Degrees it is Used in:

Electrical Engineering: The Two-Way First-Order Network Equations are widely employed in electrical engineering to design and analyze electronic circuits, audio systems, and signal processing applications.
Audio Engineering: In audio engineering, these equations play a pivotal role in designing crossover networks for speakers to ensure optimal performance and frequency response.
Acoustics: Acoustics professionals utilize these equations to create precise frequency responses in speaker systems, contributing to accurate sound reproduction in different settings.
Digital Signal Processing (DSP): These equations are essential for implementing digital filters, analyzing audio signals, and optimizing frequency responses in DSP tasks.
Telecommunications: The Two-Way First-Order Network Equations are used in telecommunications to design filters in communication systems, facilitating efficient signal processing and frequency separation.

Real-Life Applications:

Speaker Systems: The Two-Way First Order Network Equations are crucial in designing crossover networks for speakers, ensuring balanced audio output.
Noise Cancellation Headphones: These equations create filtering systems for noise-cancellation headphones, which provide users with a quiet listening experience in noisy environments.
Audio Equalizers: The equations help adjust frequency levels for tailored audio output in recording studios and music production.
Telecommunication Networks: Engineers utilize these equations to design filters for communication systems, optimizing signal processing and noise reduction in wireless networks.
Automotive Audio Systems: The equations help design crossover networks for car speakers, enhancing audio performance in vehicles.

Common Mistakes:

Mixing up the low-pass and high-pass filter component values.
Incorrectly calculating the frequency for which the crossover is designed.
Neglecting the impact of component tolerances on the crossover network performance.
Failing to consider the impedance of the speaker drivers when designing the crossover.
Overlooking the physical size and power handling capacity of the components used in the crossover.

Frequently Asked Questions:

Q: What are the key differences between first-order and higher-order crossover networks?
A: The key difference lies in the slope of the roll-off in the frequency response. Higher-order crossover networks have steeper roll-off characteristics compared to first-order networks.
Q: Can I use the same values for capacitor and inductor in both the high-pass and low-pass filters of a two-way speaker system?
A: No, the capacitor and inductor values will vary for the high-pass and low-pass filters to achieve the desired crossover frequency and response characteristics.
Q: How do the component values influence the speaker system's crossover frequency and frequency response?
A: The component values directly affect the speaker system's crossover frequency and frequency response. Higher capacitance or inductance values lead to lower crossover frequencies and vice versa.
Q: Can I use off-the-shelf capacitors and inductors to design crossover networks?
A: Yes, off-the-shelf components can be used, but the tolerance and quality of the components must be considered to ensure accurate crossover performance.
Q: How important is it to measure and match the actual values of capacitors and inductors for precise crossover design?
A: Measuring and matching the actual values is crucial, especially for high-fidelity audio systems, as slight variations in component values can significantly impact the crossover performance.

Passive Crossover Design Calculator

Two Way First Order Network Equations